June 2019, Vol. 246, No. 6
Features
Modeling and Prediction of Black Powder Erosion of Gas Pipelines
By Ehab Elsaadawy and A.M. El-Sherik, Saudi Aramco, Research & Development Center, Dhahran, Saudi Arabia
Black powder is composed of different forms of iron sulfide (FeS), iron oxides (Fe3O4, FeOOH) and iron carbonate (FeCO3), mechanically mixed or chemically combined with any number of contaminants, such as salts, sand, liquid hydrocarbons, metal debris, and even naturally-occurring radioactive material (NORM).

Black powder particles are jagged and harder than many engineering materials used in pipelines and pipeline components and hence can be very erosive. Using Vickers micro-hardness technique, the hardness of Fe3O4 black powder particles was measured to be equivalent to 52 Rockwell C as compared 89 Rockwell B for carbon steel.
Figure 1a and b show scanning electron microscope image of black powder particles and carbon steel control valve cage that was eroded by black powder after 45 days in service.
Analysis of a large number of black powder samples collected from the Saudi Aramco sales gas system showed that magnetite (Fe3O4) makes approximately 80wt% of black powder composition.
Hardness measurements conducted on the black powder particles and analytical grade Fe3O4 powder (98% purity) using the nano-indentation technique revealed similar hardness values. On the basis of these studies, Magnetite (Fe3O4) powder was considered a reasonable substitute.
In an earlier work, we experimentally investigated the erosion resistances of different materials under the erosion effects of magnetite powder and the correlation developed for A-53B carbon steel was employed in the current simulations to predict the erosion rates of pipeline bends made of A-53B carbon steel.
Mathematical Model
In gas transmission pipelines, the black powder particles volumetric loading ratio is very small, typically less than 10%, therefore, the flow can be dealt with as dilute gas-solid two-phase flow and hence the continuous phase, gas, can be modeled using the Eulerian approach while the dispersed phase, particles, using the Lagrangian approach.
For the continuous phase, gas, the Reynolds averaged Navier-Stokes (RANS) equations for steady, incompressible, and isothermal flow, specifically; the continuity and momentum equations were solved. To resolve the flow turbulence, the standard k-ɛ turbulence model with enhanced wall functions was used as well. A commercial CFD software package was used to solve this mathematical model.
The Lagrangian approach is based on the calculation of the trajectory of several individual solid particles through the flow field. The particle trajectory is determined by integrating the force balance on the particle applying Newton’s second law.
For small particles with a density much higher than that of the gas, only the drag and the gravitational settling forces will impact the trajectory of the particle while other forces (added mass, Brownian diffusion, Saffman lift and Basset force) will be negligibly small. Along a particle trajectory, the equation of motion, to be integrated, can be reduced to the following form.
Where ρp is the particle density, ρ is the gas density, g is the gravitational acceleration, and v is the gas velocity. The drag force per unit mass can be expressed as FD=(18μ/ρpd2p) (CDRep/24) where μ is the gas dynamic viscosity, Rep is the particle Reynolds numberRep=(ρdp |vp−v|)/μ , and CD is the drag coefficient. Along with the RANS and in order to predict erosion rates, a Finnie-based erosion model, Equation (2), was also solved.
where Rerosion is the erosion rate given in units of mass of target material removed per unit area per unit time, m. p is the particles mass flow rates, and Aface is the area of the cell face at the wall. The functions C(dp) and g(α) must be specified in consistent units to build a dimensionless group with the relative particle velocity and its exponent.
In the current study, five simultaneous particles injections, representing actual field conditions and were released from the flow inlets to be tracked.
Geometry, Flow Conditions
The pipeline bend under study is a standard 90-degree bend with a 36-inch (0.9-meter) pipe diameter, D. The ratios studied of the bend radius of curvature, R, to the pipeline diameter are 1.5 and 3.0. The bend has a 240-inch (6.0-meter) inlet horizontal pipe an 80-inch (2.0-meter) vertical outlet pipe. The bulk gas velocities, vB studied are 5, 10, and 20 m/s.
The gas phase used in the current study is a typical Saudi Aramco natural gas with a mass density, r, of 61.8 kg/m3 and a dynamic viscosity, m, of 1.33x1-5 Pa.s. The gas flow rates considered resulted in bulk gas velocities, vB of 10, and 20 m/s. The black powder (Magnetite) has a mass density, ρp of 5150 kg/m3 and was released at a rate of 2.4x10-3 kg/s into the stream.
Results
The gas phase and magnetite particles velocity profiles at two different planes (30 and 60 deg.) of a R/D=3.0 bend (Figure 2). The figure shows that particles follow the gas with negligible slip except at the 60 deg. plane where they deviate noticeably close to the outer wall of the bend. The gas decelerates at that wall due to the adverse pressure gradient while particles lag in response and continue to move with higher velocities.
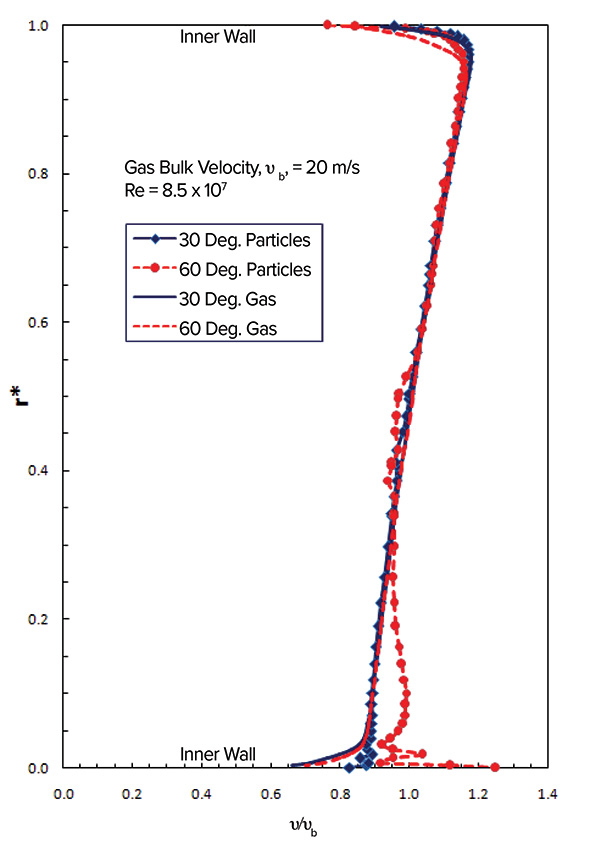
Although the inner wall of the bend encounters higher velocity stream, it is the outer wall of the bend that encounters higher erosion rate due to the impact angles of particles (Figure 3), which presents a comparison between the contours of erosion rates for a bend with R/D=3.0 at different bulk gas velocities (5, 10, and 20 m/s). Agreeing with the intuition and literature, the higher the bulk gas velocity the higher the erosion rate was.
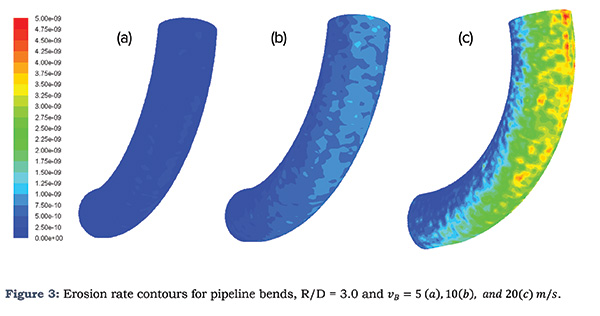
However, it should be noticed that the erosion is spreading over a wide area of the bend wall and also its value is very small. The maximum erosion rate values expressed in material thickness loss per year (Table 1).
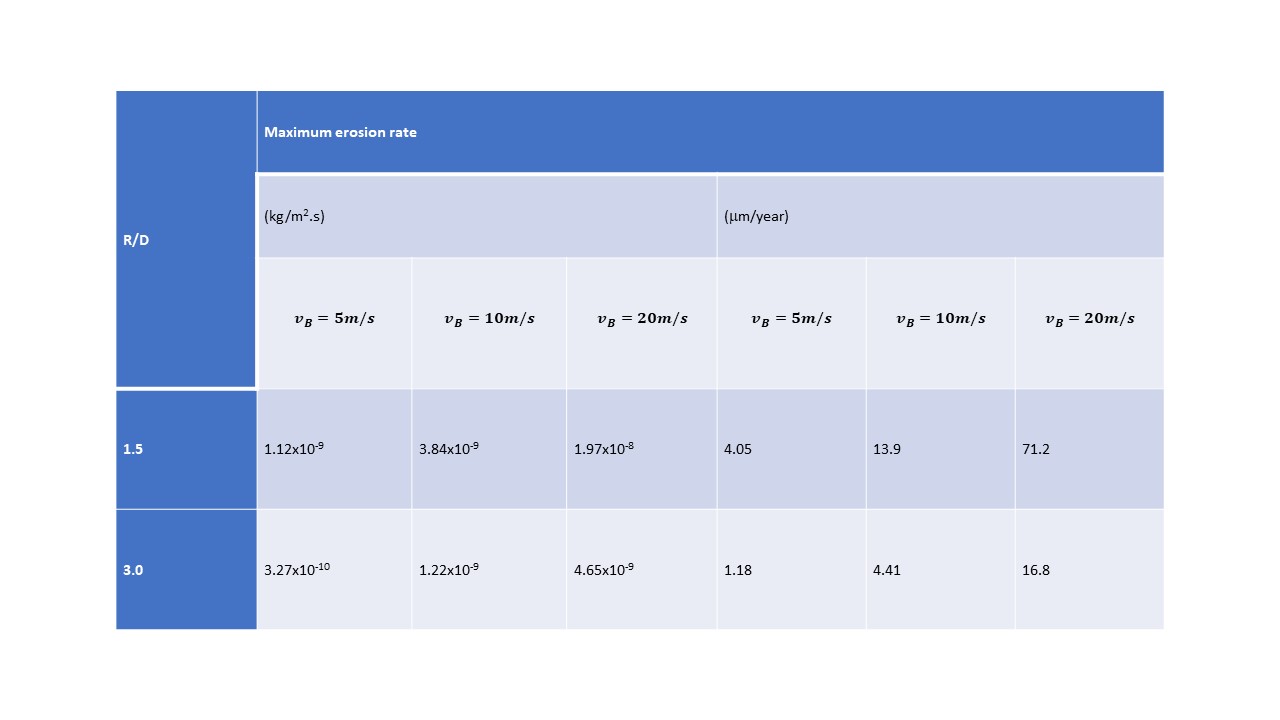
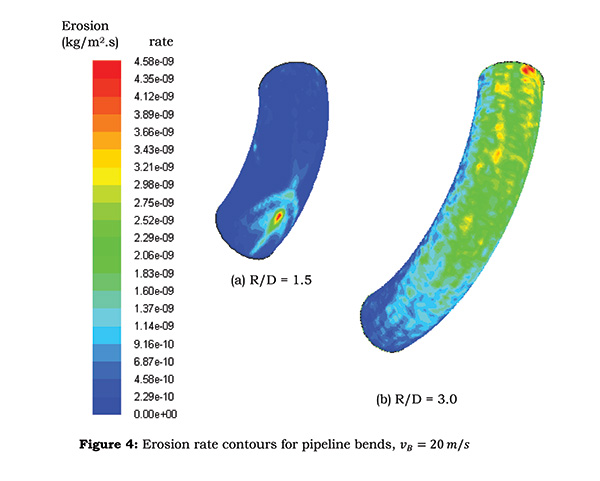
The erosion contours predicted for a bend of R/D=1.5 show concentrated erosion in smaller region, Figure 4(a), where the maximum erosion takes place at the midpoint, along the symmetry plane, of the bend where velocity profiles start showing flow reversal behavior.
This maximum value is higher than that of the R/D=3.0 bend (Figure 4(b)). Consequently, using a longer radius of curvature pipeline bend redistributes the erosion rates more uniformly over the outer wall area of the bend as compared to the shorter radius of curvature bend.
The maximum erosion rates due to black powder encountered in the current study and as summarized in Table 1 were found to be practically negligible. For instance, for a bend made of A-53B carbon steel alloy and R/D=1.5 at a maximum bulk gas velocity of 20 m/s, the erosion rate translated into a material thickness loss is 71.2µm per year (i.e. 7.12 mm in 100 years).
Conclusions
Flow and erosion of black powder particulates carried into a sales gas stream at low particles to gas mass ratios were modeled using CFD.
For pipeline bends, although the erosion rate is negligibly small under the conditions studied, a pipeline bend with longer radius of curvature will have a more uniformly distributed erosion over the outer wall of the bend, which makes it a better candidate for applications with erosive type of service such as sale gas pipelines containing black powder particles. P&GJ




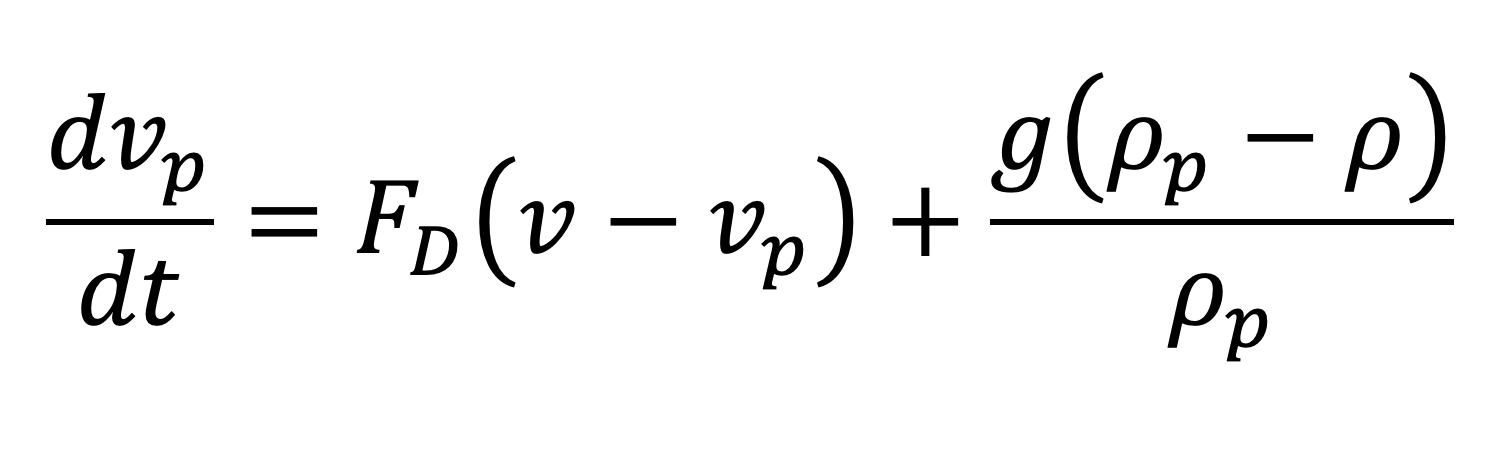
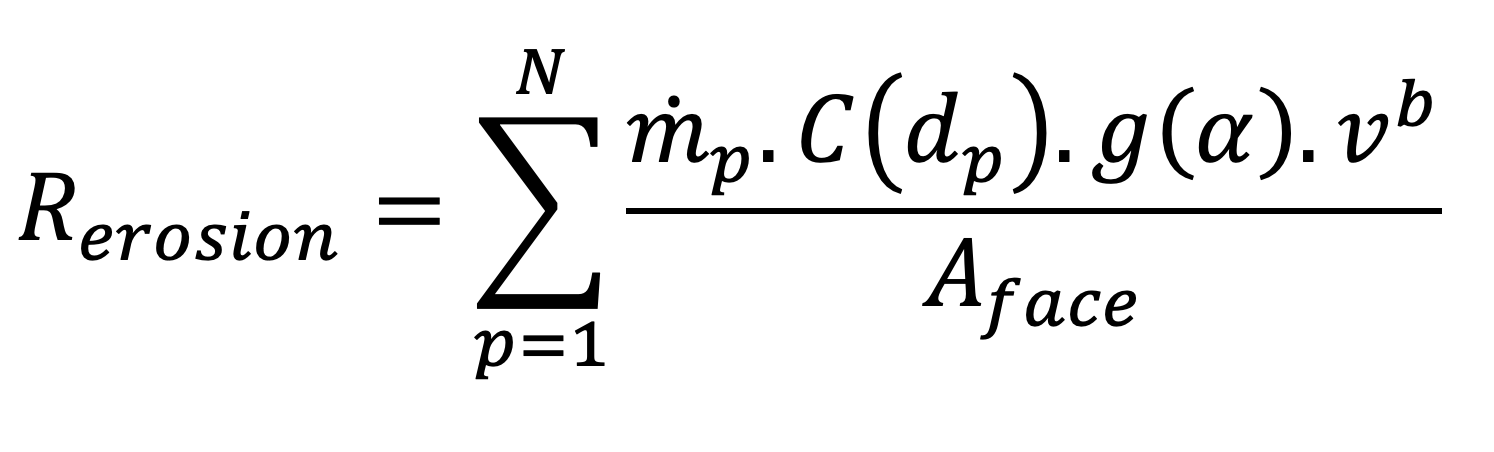


Comments